Ma.09.　次元削減

今回の分析(naiman)では、変数が340個もあり、正直うんざりするほどの質問数です。
さらに言えば、構造化されていない（理論的に整理されていない）質問群なので、どのように変数を扱えばよいのかが分かりにくい、という難しさがあります。
例えば、q3（生活満足）、q4（生活不満）、q30（環境不満）といった質問群は、そもそも一つのまとまりを持った構成になっているのか？という壁に突き当たります。

項目がある程度系統立っているかどうかを確認するだけなら、α係数やKMOなどの指標（因子分析の指標）をチェックすれば、おおよその感触をつかむことはできます。
ただし、「だからどうなんだ？」という次の壁がやってきます。
つまり、自分はこのデータの背景を理解したいのか、それとも上手に要素を取り出して活用したいのか——どちらを目的としているのかを、はっきりさせる必要があるのです。

このように考えることは、主成分分析（PCA）と因子分析（FA）という前提と成果物の性質が異なる、しかし結果が似ている分析方法の選択に役立ちます。

個人的に以下の特徴を考えて、分析方法を選択します。

• 主成分分析は、できるだけ情報を失わないように次元を縮約し、後続の分析や活用に使える新しい変数（主成分）を生成する。
• 因子分析は、観測項目の背後にある構造や潜在因子を理解するためのモデルを構築し、その構造を可視化する。

つまり、結果を使いたいならPCA、構造を理解して終わりたいならFAという理解です。
心理や社会調査の領域では、概念を理解することが目的になるため、FAが主に使われます。

一方で、今回はPCAを行い、その結果を活用する方向に舵を切ってみたいと思います。
その理由は、主成分分析で得られる変数は、演習の後半の自由な分析にも応用できるからです。

課題的に取り組んでみる

今回はq30環境不満（6問構成）の次元削減にトライしましょう。
現状、6問の回答はそれぞれが独立しているように見えるため、加算も適切ではない気がするし、それぞれの得点をそのまま解釈するしかなさそうです。
「住んでいる地域の環境に満足しているか？」ということを聞いているのだろうと、感じるのですが、現状では6問のまとまりとして考えられません。

ということで、この6問の活用方法を考える作業の一環として主成分分析に取り組んでいきたいと思います。
まずは、これらの相関行列を作ってみましょう。

library(corrplot)
cor_mat2 <- cor(df_kankyo, method = "spearman")
corrplot.mixed(cor_mat2,
               upper = "color",
               lower = "number", 
               tl.pos = "lt")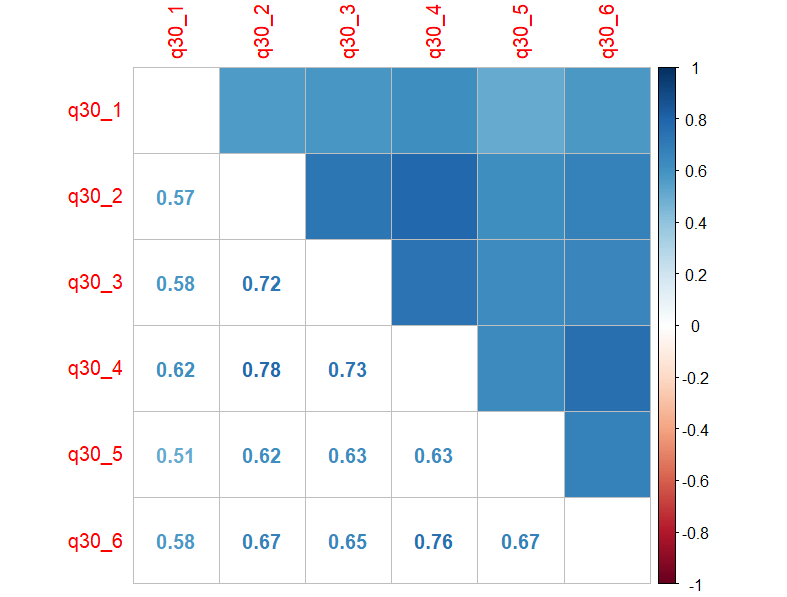

次に、dfsummaryをつかって、それぞれの得点、ヒストグラムをチェックしましょう。

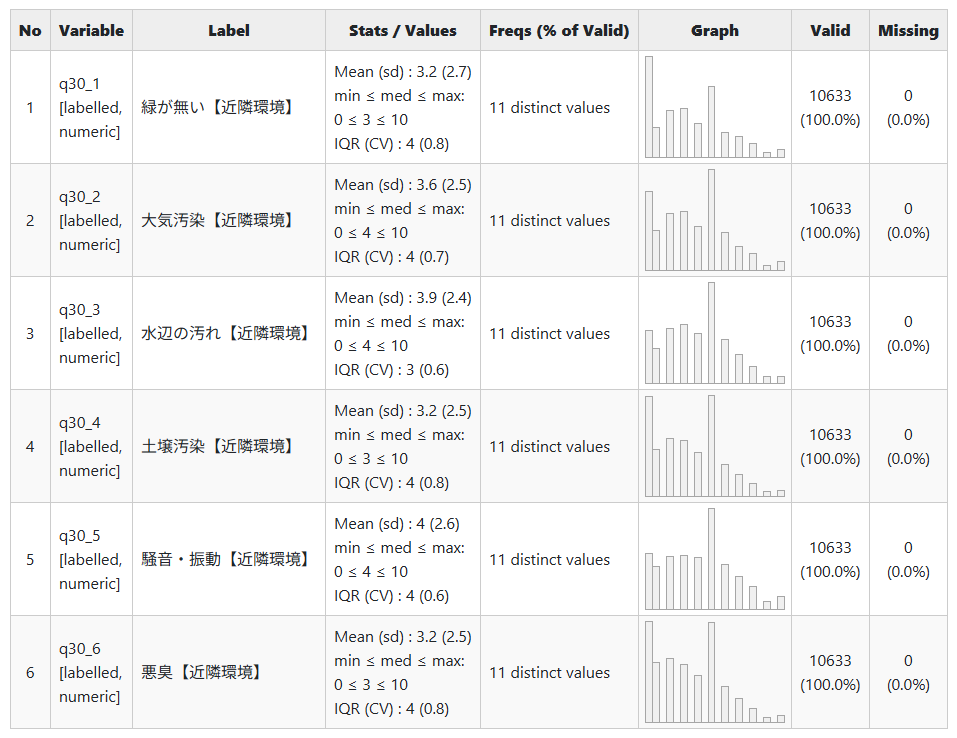
回答結果から色々と思うことはありますが、
これらの探索、そして、再び質問紙をよく読むと、これらはいくつに分けられると考えられますか？
まずは、ここがスタートだと思います。

なお、主成分分析でも（因子分析でも）、だいたい1主成分は、すべての項目を要約したような成分（スケーリングファクター）である場合が多いです。
そう考えると、あといくつの成分が取れると想像するか、ここが重要な点だと思っています。

あなたの回答

それぞれの要素は、どのような特徴を持つと、想像しますか？

さて、そのようになるかを確かめてみましょう。
コードはたったの3行です。

kankyopca <- prcomp(df_kankyo, scale=T)　#主成分分析を実施する（prcomp(df, 方法）)
summary(kankyopca) 
kankyopca$rotation #固有ベクトル（主成分軸の係数）の算出

prcomp()　→　主成分分析を実行する
scale = TRUE：各変数を「平均0・標準偏差1」に標準化してから計算します。
　　　→ 単位や桁の違う変数が混ざっていても、公平に重みづけされます。

summary(kankyopca) の見方
Standard deviation：各主成分の広がり（＝情報量の大きさの目安）
Proportion of Variance：各主成分がデータのばらつきの何割を説明しているか（＝寄与率）
Cumulative Proportion：上から何番目まで足し合わせると何割説明できるか（＝累積寄与率）

pca $ rotation （＝「主成分軸の係数」）
行：元の変数、列：主成分（PC1, PC2, …）、値：その主成分における重み（係数）
絶対値が大きいほど「その変数がその主成分を強く表している」。
符号（＋/−）は「一緒に増減するのか、反対に動くのか」の方向を示します。

FAでは、同じような段階で、係数を見ながら、主成分（因子）それぞれに名前をつけます。
PCAでも同じようにつけるのかは不明ですが、それぞれに名前をつけてみてください。
この際、たいていPC1はスケーリングファクター、PC２以降は解釈して名前をつけられると思います。
この作業は、累積寄与率が9割近くとれるところまでで十分だと思います。（さすがに元の変数の数と同じ数取るのは非効率）

解釈を２次元の図で助けることも可能です。
特にPC2とPC3の関係性を図示できると理解が深まります。

biplot(kankyopca, choices = c(2, 3))

このようにすると、６個の質問が、PC2、PC3の上でどのような働きをしているかを診ることができます。

振り返り、活用する方法を考える。

ここまでを振り返ると、たったの３行で以下の３点において、進んだといえる。
1. どのような主成分があるかが知れた。
2. それぞれの成分によって、6問の何％が説明できるかを知れた。
3. 6項目から上手に重み付けをしたスケーリングファクターの得点が利用可能になっている。
　　（妥当性が検討されていないが、単純に加算するよりもPC１は「環境不満」をうまく表しているだろうと期待）

では、最後に、これをもとのDfに戻す方法を知る必要があります。
主成分分析は使う分析だということを考えると、
それぞれの回答者の得点をkankyo_PC1のような変数としてお返ししなくてはいけません。

まずは各回答者の得点を上から順に算出する。

pcascore <- kankyopca$x
pcascore <- as.data.frame(pcascore)
pcascore <- pcascore %>%
  rename_with(~ paste0("kankyo_", .x))

1. pcascore <- kankyopca$x
   → PCAのスコア行列（各サンプルのPC1, PC2, …の値）を取り出す。
2. pcascore <- as.data.frame(pcascore)
   → データフレーム化（列名は通常 “PC1”, “PC2”, …）。
3. rename_with(~ paste0("kankyo_", .x))
   → すべての列名の先頭に "kankyo_" を付ける
   例：PC1 → kankyo_PC1

それをそのまま元のDfに入れ込む（丁寧ではないが）。
IDとか、欠損値処理とか、そういうことをここでは一切していないので、行に矛盾がでることを想定していません。
投入後、Head, Tailではみ出たり、不足が出ていないかチェックして下さい

naiman_with_pca <- naiman_c12 %>%
  bind_cols(pcascore)

ここで生成された変数は、これは、q4s9_1（生活環境への不安）と関連するはず…。（なのに）